
Kein Problem und keine Mathematik
Der Showmaster sagt zur Kandidatin: Wenn Sie nicht Tür 1 nehmen, gebe ich ihnen Tür 2 und 3 dafür. Sie dürfen dann beide öffnen.
Um es gleich zu sagen: Diese Abwandlung des Spielverlaufs beschreibt im Prinzip das, was passiert, wenn die Kandidatin wechselt. Wechselt man, ist es so, als bekäme man nicht nur eins, sondern zwei Tore, die man dann beide öffnen darf! Der Wechsel verdoppelt also die Chancen. So ein Angebot würde doch niemand ablehnen, oder? (Mehr dazu weiter unten.)
Inhalt
Viele kennen es schon, das sogenannte Ziegenproblem: In der Fernsehshow Let‘s make a deal (Geh‘ aufs Ganze) muss ein Kandidat eine von 3 Türen wählen, hinter der er sich einen Gewinn erhofft. Danach öffnet der Showmaster eine der beiden anderen Türen, hinter der sich eine Niete (Ziege) befindet, und fragt den Kandidaten, ob er bei seiner Wahl bleibt oder nicht lieber zur dritten, noch verschlossene Tür wechselt. Der kann sich jetzt fragen:
Soll ich bei meiner Wahl bleiben?
Ist es besser, zu wechseln?
Oder ist es egal, weil die Chancen so oder so 50:50 stehen?
Die meisten Menschen sind der Meinung, es ist besser, zu wechseln.
Der Einspruch der Skeptiker
Doch Skeptiker sagen: Es ist egal, also fifty-fifty oder sogar von Nachteil, denn man könne nie wissen, welche Strategie der Spielleiter hat, ob er parteiisch oder unparteiisch ist. Theoretisch könnte er manipulativ sein, und diesen Faktor dürfe man nicht ignorieren.
Doch welchen Spielraum könnte der Showmaster haben, der es ihm erlaubt, eine „Strategie“ anzuwenden? Schließlich öffnet er bekanntlich immer eine Tür mit einer Ziege. Es ist also nicht so, dass er dem einen Kandidaten den Tausch anbietet und einem anderen nicht. In diesem Fall wäre die durchschnittliche Gewinnwahrscheinlichkeit vielleicht tatsächlich 50:50.
Alles, was er tun könnte, wäre, die Kandidaten unterschiedlich stark zum Wechsel zu drängen. Eine Kandidatin, die das richtige Tor bereits gewählt hat und ihm sehr sympathisch ist, wird er wahrscheinlich nicht wiederholt fragen: „Wollen sie nicht doch lieber zum anderen Tor wechseln?“ Bei einem ihm unsympathischen Kandidaten macht er das vielleicht doch schon mal.
Und selbst wenn er unparteiisch ist (oder zumindest glaubt, es zu sein), könnte er unbewusst Signale aussenden, die den Kandidaten/die Kandidatin beeinflussen.
Doch würde der Spielleiter das tatsächlich tun, hätte das schon längst jemand bemerkt. Warum, erkläre ich am Ende dieser Seite.
Gruppenaufteilung, Schalen-Variante und tabellarische Betrachtung
Diese drei Darstellungsformen zeigen auf unterschiedlichen Wegen, was passiert, wenn der Showmaster eine Tür öffnet oder die Kandidatin wechselt oder bei ihrer Wahl bleibt.
Die Gruppenaufteilung
Die Kandidatin wählt Tor 1. Anschließend teilen wir die Tore in Gruppen ein. Aus dem gewählten bilden wir Gruppe A, aus den nicht gewählten Gruppe B.
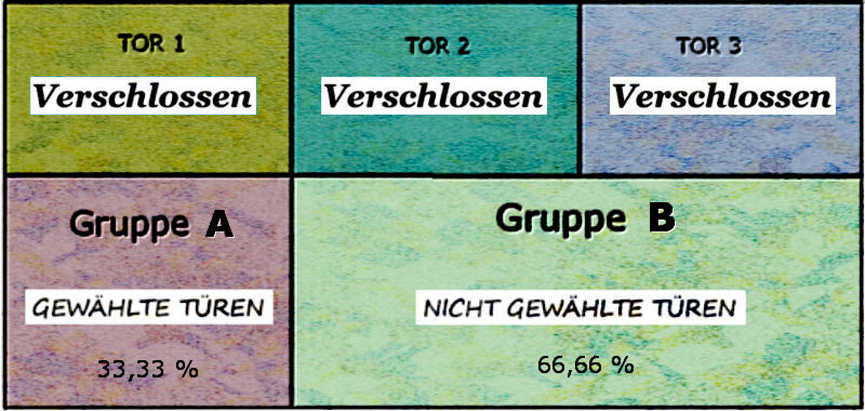
Man sieht sofort: Die Wahrscheinlichkeit, dass der Gewinn in Gruppe B ist, ist doppelt so hoch wie für Gruppe A. Doch würde die Kandidatin in dieser Situation zur Gruppe B wechseln, hätte sie noch zwischen Tor 2 und 3 zu wählen, was die Gewinnwahrscheinlichkeit wieder auf 1/3 reduziert.
Der Kandidat wechselt nicht die Tür, sondern die Gruppe
Öffnet der Showmaster jedoch zuvor ein Tor mit einer Niete in Gruppe B, fällt dieser zweite Wahlvorgang weg, die Gewinnwahrscheinlichkeit für Gruppe B bleibt jedoch bei 2/3. Denn warum sollte sie sich ändern? Sie wurde zu Beginn des Spiels festgelegt und kann sich deshalb (durch das Öffnen eines oder auch aller Tore) unmöglich ändern.
Vor dem Öffnen hatten Tor 2 und 3 einzeln je eine Wahrscheinlichkeit von 1/3 und gemeinsam 2/3. Nach dem Öffnen besitzen sie gemeinsam immer noch 2/3, auch wenn eins davon inzwischen geöffnet ist. Das geöffnete hat jetzt den Wert Null (sozusagen 0/3) und das geschlossene dafür den Wert 2/3.
Wenn Tor 2 eine Niete ist, gibt es immer noch eine 2. Chance, dass Tor 3 das nicht ist. Der Tod des 2. Tores hat die Wahrscheinlichkeit, dass Tor 3 keine Niete ist, verdoppelt. Tor 3 hat den Wahrscheinlichkeitswert des 2. Tores sozusagen geerbt und ist ab jetzt der alleinige Wahrscheinlichkeitsträger in Gruppe B.

Zwei Türen im Tausch gegen eine
Stell dir ein Spiel vor, bei dem man von 3 Losen 1 Los auswählen muss. Danach darf man – wenn man will – dieses Los gegen die beiden anderen eintauschen. Tut man das, ist es im Prinzip so, als hätte man von 3 Losen das Los bestimmt, das man nicht haben will.
Öffnet der Moderator Tür 2, besteht Gruppe B nur noch aus einer wählbaren Tür, obwohl ihr Wahrscheinlichkeitswert zwei repräsentiert. Wenn man will, kann man den Vorgang auch so beschreiben:
Der Moderator bietet der Kandidatin zwei Türen zum Tausch an, von denen er eine bereits aus der Konkurrenz genommen hat. (Die geöffnete gibts sozusagen als Anschauungsobjekt gratis dazu. Sie ist zwar für nichts gut, schaden tut sie aber auch nicht.)
Noch deutlicher zeigt es dieser Spielablauf: Anstatt dass der Spielleiter Tür 2 öffnet und die Kandidatin die Möglichkeit bekommt, zu Tür 3 zu wechseln, bietet er ihr an, Tür 1 direkt gegen die beiden anderen einzutauschen, die sie dann auch beide öffnen darf. Denn:
Ob die Kandidatin zweimal eine Tür öffnet und es ihr dabei erlaubt ist, einmal eine Niete zu erwischen, oder ob der Spielleiter diese Niete für sie zuvor aussortiert und sie dann nur noch eine Tür zu öffnen hat, ist völlig egal. Verstanden?
Wenn die Kandidatin wechselt, ist es in Prinzip das Gleiche, als dürfe sie 2 Türen wählen und dann auch beide öffnen.
Was Skeptiker nicht verstehen
Manche Skeptiker sagen jedoch: Solange der Spielleiter noch kein Tor geöffnet hat, ist die Wahrscheinlichkeit für Gruppe B tatsächlich 2/3 Prozent. Doch sobald er eins öffnet, wäre das nicht mehr so! Dann wäre die Wahrscheinlichkeit für die beiden noch verschlossenen Tore fifty-fifty.
Doch würde nach dem Öffnen eines Tores die Wahrscheinlichkeit tatsächlich 1:1 sein, hätte das vor dem Öffnen auch schon so sein müssen, denn der Spielleiter öffnet ja immer ein Tor mit einer Ziege. Und das bedeutet: Es ist egal, ob das Tor mit der Ziege bereits geöffnet ist! Allein das Wissen, dass ein Tor mit einer Ziege geöffnet werden wird, ist ausreichen. Das Tor mit der Ziege ist vor dem Öffnen sozusagen „virtuell“ bereits geöffnet. Es war nur noch nicht bekannt, welches es ein wird – doch das ist vollkommen egal. Verstanden?
Die Schalen-Variante
Stell dir folgendes Spiel vor:
Auf einem Tisch stehen 2 Schalen. In der linken liegt 1 Los und in der rechten liegen 2. Eins der drei Lose ist der Gewinn eines Autos, die beiden anderen sind Nieten.
Nur der Spielleiter weiß, welches Los gewinnt. Dann entfernt er eine Niete aus der rechten Schale und fordert die Kandidatin auf, ein Los/eine Schale zu wählen.
Sollte sich der Gewinn tatsächlich in der rechten Schale befinden (was in 2 von 3 Fällen der Fall ist), besteht immer noch die fünfzigprozentige Gefahr, die Niete zu erwischen. Entfernt der Showmaster diese Niete, besteht diese Gefahr jedoch nicht mehr. Das Entfernen einer Niete aus der rechten Schale entspricht dem Öffnen einer Tür.
Bei diesem Spielablauf geschieht das Gleiche wie bei dem mit den Türen und den Ziegen. Es sollte leicht zu erkennen sein. Im Prinzip ist es dasselbe Spiel, nur auf eine andere Art gespielt.
Die Schalen-Variante veranschaulicht jedoch gut, warum sich durch das Öffnen einer Tür die Wahrscheinlichkeiten für die anderen nicht ändern können: Entfernt der Spielleiter eine Niete aus der rechten Schale, verändert das nicht die Verteilung der Lose in den Schalen (denn nur dann wäre eine Veränderung der Wahrscheinlichkeiten möglich, sodass man sagen könnte, die Gewinnwahrscheinlichkeit liegt jetzt bei 50:50). Es bleibt bei der Wahrscheinlichkeitsverteilung von 1/3 für die linke und 2/3 für die rechte Schale (und nicht 1/2 für die linke und 1/2 für die rechte), auch wenn die inzwischen nur noch 1 Los enthält.
Die unsichtbaren Schalen
Ändert man die Schalen-Variante etwas ab, sieht man, dass es sogar egal ist, ob dieses Spiel mit oder ohne Schalen gespielt wird (wie es bei der Tür-Variante der Fall ist). Allein das Wissen darüber, dass ein Los entfernt wurde, hilft uns weiter:

Welches Los würde du wählen, nachdem nur noch 2 Lose ohne Schalen auf dem Tisch liegen?
Auf einem Tisch stehen 2 Schalen. In der linken liegt 1 Los und in der rechten liegen 2. Eins der drei Lose ist der Gewinn eines Autos, die beiden anderen sind Nieten. Nur der Spielleiter weiß, welches Los gewinnt.
Nun die Abwandlung:
Der Spielleiter nimmt die Lose aus den Schalen heraus und legt sie vor die Schalen auf den Tisch. Vor der linken Schale liegt jetzt 1 Los und vor der rechten liegen 2.
Dann entfernt er ein Los (eine Niete), das vor der rechten Schale liegt und nimmt auch die Schalen vom Tisch.
Jetzt liegen also nur noch zwei Lose auf dem Tisch. Jemand, der erst jetzt hinzukommt und nicht weiß, was zuvor geschehen ist, wird denken müssen, dass die Wahrscheinlichkeit für beide Lose gleich ist. Doch für Los 2 ist die Gewinnwahrscheinlich doppelt so hoch wie für Los 3.
Wer also glaubt oder der Meinung ist, nach dem Öffnen der 2. Tür wären die Wahrscheinlichkeiten 50:50, verhält sich wie jemand, der nicht weiß, wie es dazu kam, dass vor ihm zwei scheinbar gleichberechtigte Lose auf dem Tisch liegen.
Die tabellarische Betrachtung
Die tabellarische Aufstellung macht es ebenfalls deutlich. Wir wissen, im Durchschnitt wird jede Kandidatin/jeder Kandidat bei jedem 3. Spiel sofort das richtige Tor wählen. Davon lässt sein ableiten:

Aus statistischer Sicht ist es also immer vorteilhaft, zu wechseln: Zweimal pro drei Spiele wählt der Kandidat eine Ziege, doch er wechselt und bekommt das Auto. Doch nur einmal pro drei Spiele bekommt er das Auto, wenn er nicht wechselt.
Kein mathematisches Rätsel – nur eine assoziative Täuschung
Ich betrachte das Ziegenproblem deshalb nicht als mathematisches Rätsel (als das es manchmal bezeichnet wird), sondern eher als eine Art der assoziativen Täuschung – im Sinn einer optischen Täuschung. Im Grunde genommen ist es einfach, doch das Öffnen der Tür verwirrt uns – ohne dass wir es merken. Es ist wie bei einem Illusionisten, der mit überflüssigen Bewegungen und allerlei Schnickschnack unsere Aufmerksamkeit vom wirklichen Geschehen ablenkt.
Unser Fehler ist, zu glauben, wir hätten durch das Öffnen einer Tür zusätzliche Informationen erhalten: Wir denken, jetzt etwas zu wissen, das wir zuvor nicht wussten. Doch das stimmt nicht!
Wir wissen jetzt zwar, hinter Tür 2 verbirgt sich eine Ziege, doch indirekt wussten wir das vorher auch schon: Wir wussten, entweder Tür 2 oder 3 muss eine Ziegentür sein. Wir wussten nur nicht, welche. Öffnet der Spielleiter Tür 3, wechseln wir zu Tür 2, öffnet er Tür 2, wechseln wir zu Tür 3. Es ist gleichbedeutend und austauschbar. Eine von beiden Türen musste es sein und aus diesem Grund ist es völlig unwichtig, welche es ist. Verstanden?
Die siamesischen Türen
Wenn wir also wissen, Tür 2 ist eine Ziege, ist es dasselbe, als wüssten wir, dass Tür 3 eine Ziege ist. Deswegen hilft uns das Wissen, hinter welcher Tür sich eine Ziege verbirgt, nicht weiter, denn in dieser Phase des Spiels sind Tür 2 und 3 im Prinzip miteinander identisch: Sie fungieren zunächst nur als Platzhalter für die aufzudeckende Ziege in Gruppe B.
Doch wenn der Moderator eine Tür öffnet und somit die Anzahl der wählbaren Türen auf zwei reduziert, lassen wir uns irritieren. Wir glauben, jetzt mehr zu wissen und es nur noch mit zwei Türen zu tun zu haben und dass sich die Wahrscheinlichkeiten für diese neu berechnen. Vorher hatten wir drei Türen zu je 1/3, jetzt haben wir zwei zu je 1/2 – denken wir. Doch das wäre nur dann der Fall, hätte die Kandidatin nicht zuvor eine Tür gewählt.
Zwei mögliche Szenarien
- Szenario:
Würde der Moderator Tor 2 öffnen, bevor die Kandidatin ein Tor wählt, wären die Wahrscheinlichkeiten für Tor 1 und 3 tatsächlich gleich hoch:
Von drei Toren, von denen jedes 1/3 Gewinnwahrscheinlichkeit besitzt, wird ein Verlierer-Tor entfernt und aus der Konkurrenz genommen. Es gibt jetzt nur noch zwei Tore. Diese bilden zusammen jetzt 100 Prozent. Jedes Tor bekommt die Hälfte.
- Szenario:
Im 1. Szenario reduziert der Moderator die Tore einfach von drei auf zwei – mehr passiert nicht. Das eigentliche Spiel beginnt erst danach.
Doch wenn der Kandidat Tor 1 wählt, bevor der Showmaster Tor 2 öffnet, ist die Situation eine andere: Es sind dann immer noch drei Tore im Spiel: 2 geschlossene und 1 geöffnetes. Das geöffnete ist zwar kein wählbares mehr, aber das spielt keine Rolle.
Der manipulative Showmaster
Oben stehende Beobachtungen und Überlegungen gehen davon aus, dass der Showmaster natürlich immer eine Tür öffnet (andernfalls hätte die Aufgabenstellung keinen Sinn und soweit ich weiß, wurde das Spiel auch nie anders gespielt) und die Kandidatin selbstverständlich nicht manipuliert, also vollkommen neutral ist und niemanden suggestiv beeinflusst.
Doch nehmen wir einmal an, er tut es doch – absichtlich oder unbewusst. Es ist interessant, dass auch dann der Wechsel zum anderen Tor aus statistischer Sicht die Gewinnchance verdoppelt.
Der konfuse Kandidat
Wenn der Showmaster den Kandidaten manipuliert, bedeutet das nicht automatisch, dass es ihm immer gelingt. Schließlich darf er dem Kandidaten/der Kandidatin keine offensichtlichen Zeichen geben. Das würde schnell jemand mitkriegen. Deshalb müsste er sehr subtil vorgehen. Trotzdem müssen seine Signale gut verständlich sein – andernfalls verlieren sie ihre Wirkung.
Manipuliert der Spielleiter den Kandidaten, wird dieser die Hilfe (oder scheinbare Hilfe, die ins Verderben führt) deshalb nicht immer bemerken. Oder er wird die subtilen Hinweise falsch interpretieren und das Gegenteil tun. Und manchmal wird er nur denken, der Showmaster gibt ihm heimliche Tipps und sich dann anders entscheiden, als er es sonst getan hätte, denn in einer Welt, in der der Showmaster korrupt ist, wird auch das passieren. Das alles kann zum Vorteil oder Nachteil der Kandidatinnen und Kandidaten sein.
Niemand der Zuschauer dürfte auch nur den geringsten Verdacht haben, dort könnte etwas nicht mit rechten Dingen zugehen. Auf lange Sicht geht so etwas jedoch nie gut. Mit Sicherheit hätten aufmerksame Zuschauer in den 1960er und 1970er-Jahren das längst bemerkt und es wäre öffentlich bekannt geworden.
Alles zusammen betrachtet, würden die unterschiedlichen Szenarien sich gegeneinander aufheben und auf die Gewinnwahrscheinlichkeit keinen signifikanten Einfluss haben.
Der faule Showmaster
Eine andere bekannte Theorie ist der „faule Showmaster“, der (vielleicht unbewusst) bevorzugt das Tor öffnet, das ihm am nächsten ist. Davon lässt sich ableiten: Öffnet er das etwas weiter entfernte Tor, steckt das Auto hinter dem näheren. Denn ist das Auto hinter keins von beiden, hätte er keinen Grund, den weiteren Weg zu gehen und würde das näherliegende öffnen.
Doch auch das hätten aufmerksame Zuschauer bemerkt, denn am Ende eines jeden Spiels sind alle Tore geöffnet. Früher oder später wäre deshalb jemandem Folgendes aufgefallen: Wählt der Kandidat Tor 1 oder 2, und das Auto steckt auch dahinter, öffnet der Showmaster, wenn er auf der rechten Seite steht, immer Tor 3. Oder: Wählt der Kandidat Tor 3, und das Auto steckt auch dort, öffnet der Showmaster immer Tor 2 (also niemals Tor 1).
Eine interessante Diskussion zur Kontroverse um das Ziegenproblem findest du HIER
Einfacher so erklärt:
Wenn ich einThor („Wer Thor ohne h schreibt, ist ein Tor, Schopenhauer) gewählt habe, so sitze ich mit 2/3 auf einer Ziege. Wenn der Showmaster mir nun eine Ziege eliminiert, ist das Thor, das noch übrig bleibt, statistisch besser, weil es nur zu einem Drittel auf einer Ziege sitzt. Also wechseln.